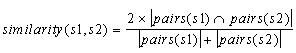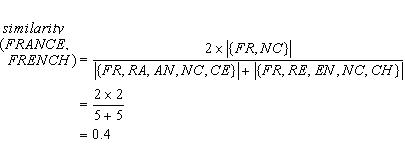Duplicate Names Search

From ICISWiki

(Reference: "How to Strike a Match". Original article by Simon White. Available at http://www.devarticles.com/c/a/Development-Cycles/How-to-Strike-a-Match/)

Existing string similarity algorithms

The Soundex Algorithm is an equivalence algorithm, so simply states whether or not two strings are similar. However, it would not recognise any similarity between ‘FRANCE’ and ‘REPUBLIC OF FRANCE’, as they start with different letters.

The Edit Distance algorithm would acknowledge some similarity between the two strings, but would rate ‘FRANCE’ and ‘QUEBEC’ (with a distance of 6) to be more similar than ‘FRANCE’ and ‘REPUBLIC OF FRANCE’ (which have a distance of 12).

The Longest Common Substring would give ‘FRANCE’ and ‘REPUBLIC OF FRANCE’ quite a good rating of similarity (a common substring of length 6). However, it is disappointing that according to this metric, the string ‘FRENCH REPUBLIC’ is equally similar to the two strings ‘REPUBLIC OF FRANCE’ and ‘REPUBLIC OF CUBA’.

A new string similarity metric

REQUIREMENTS:

• Rewards both common substrings and a common ordering of those substrings.
• Consider not only the single longest common substring, but other common substrings too.

SOLUTION: Find out how many adjacent character pairs are contained in both strings.

Excerpt from article:

The intention is that by considering adjacent characters, I take account not only of the characters, but also of the character ordering in the original string, since each character pair contains a little information about the original ordering.

Let me explain the algorithm by comparing the two strings ‘France’ and ‘French’. First, I map them both to their upper case characters (making the algorithm insensitive to case differences), then split them up into their character pairs:

 FRANCE: {FR, RA, AN, NC, CE}
 FRENCH: {FR, RE, EN, NC, CH}

Then I work out which character pairs are in both strings. In this case, the intersection is {FR, NC}. Now, I would like to express my finding as a numeric metric that reflects the size of the intersection relative to the sizes of the original strings. If pairs(x) is the function that generates the pairs of adjacent letters in a string, then my numeric metric of similarity is:

The similarity between two strings s1 and s2 is twice the number of character pairs that are common to both strings divided by the sum of the number of character pairs in the two strings. (The vertical bars in the formula mean ‘size of’.) Note that the formula rates completely dissimilar strings with a similarity value of 0, since the size of the letter-pair intersection in the numerator of the fraction will be zero. On the other hand, if you compare a (non-empty) string to itself, then the similarity is 1. For our comparison of ‘FRANCE’ and ‘FRENCH’, the metric is computed as follows:

The values of the metric always lie between 0 and 1.

Implementation in Delphi programming language

function TfrmMain.LetterPairs(s: string): TStrings;
//==============================================================================
//  The basis of the algorithm is the method that computes the pairs of characters
// contained in the input string. This method creates a LIST OF STRINGS to contain
// its result. It then iterates through the input string, to extract character
// pairs and store them in the stringlist. Finally, the stringlist is returned.
//
// REFERENCE: http://www.devarticles.com/c/a/Development-Cycles/How-to-Strike-a-Match/3/
// ("How to strike a match"; contributed by Simon White)
//
// Original JAVA implementation by Simon White; translated to Delphi by Corina Habito
//
//==============================================================================
var
 i, iNumPairs: integer;
 tsPairs: TStrings;
begin
 tsPairs := TStringlist.Create;
 tsPairs.Clear;
 iNumPairs := Length(trim(s)) - 1;
 for i := 1 to iNumPairs do begin
   tsPairs.Add(copy(s,i,2));
 end;
 Result := tsPairs;
end;

function TfrmMain.GetWordLetterPairs(const s:string;slist:tstringlist);
//==============================================================================
// This method uses the ParseDelimited method to split the input string into
// separate words, or tokens. It then iterates through each of the words,
// computing the character pairs for each word. The character pairs are added to
// a stringList, which is returned from the method. An stringlist is used,
// because we do not know in advance how many character pairs will be returned.
// (At this point, the program doesn’t know how much white space the input string contains.)
//
//
// REFERENCE: http://www.devarticles.com/c/a/Development-Cycles/How-to-Strike-a-Match/4/
// ("How to strike a match"; contributed by Simon White)
//
// Original JAVA implementation by Simon White
//   - Translated to Delphi by Corina Habito. December 6 2007.
//   - Modified May 5 2008. Thanks to John Wild (www.searchers.com) for comments.
//==============================================================================
 var
     tsWords : TStrings;
     w,i     : Integer;
  begin
     tsWords  := TStringlist.Create;
     try
        ParseDelimited(tsWords,trim(s),' ');
        for w := 0 to tsWords.count - 1 do
           for i := 1 to (Length(trim(tsWords[w]))-1)  do
              slist.Add(copy(tsWords[w],i,2));
     finally
        freeandnil(tsWords);
     end;
  end;

  procedure TfrmMain.ParseDelimited(const sl : TStrings; const value : string; const delimiter : string);
//==============================================================================
//  Tokenize the string and put words into a stringlist
//==============================================================================
var
  dx : integer;
  ns : string;
  txt : string;
  delta : integer;
begin
  delta := Length(delimiter) ;
  txt := value + delimiter;
  sl.BeginUpdate;
  sl.Clear;
  try
    while Length(txt) > 0 do
    begin
      dx := Pos(delimiter, txt) ;
      ns := Copy(txt,0,dx-1) ;
      sl.Add(ns) ;
      txt := Copy(txt,dx+delta,MaxInt) ;
    end;
  finally
    sl.EndUpdate;
  end;
end;

function TfrmMain.CompareLetterStrings(sFirst,sSecond: string): Double;
//==============================================================================
// Computes the character pairs from the words of each of the two input strings,
//   then iterates through the stringLists to find the size of the intersection.
//   Note that whenever a match is found, that character pair is removed from the
//   second array list to prevent us from matching against the same character pair
//  multiple times. (Otherwise, ‘GGGGG’ would score a perfect match against ‘GG’.)
//
// REFERENCE: http://www.devarticles.com/c/a/Development-Cycles/How-to-Strike-a-Match/4/
// ("How to strike a match"; contributed by Simon White)
//
// Original JAVA implementation by Simon White
//   - Translated to Delphi by Corina Habito. December 6 2007.
//   - Modified May 5 2008. Thanks to John Wild (www.searchers.com) for comments.
//==============================================================================
var
  tsAllPairs,
  tsPairs,
  tsP1,tsP2      : tstrings;
  tsPairs1,
  tsPairs2       : TStringlist;
  iIntersection,
  iUnion,i,j     : integer;
  sPair1,sPair2  : String;
begin
  tsPairs1   := TStringlist.create;
  tsPairs2   := TStringlist.create;
  try
     iIntersection := 0;
     GetWordLetterPairs(Uppercase(sFirst),tsPairs1);
     GetWordLetterPairs(Uppercase(sSecond),tsPairs2);
     iUnion := tsPairs1.Count + tsPairs2.Count;
     for i := 0 to tsPairs1.Count - 1 do
     begin
        sPair1 := tsPairs1[i];
        for j := 0 to tsPairs2.Count - 1 do
        begin
           sPair2 := tsPairs2[j];
           if sPair1 = sPair2 then
           begin
              iIntersection := iIntersection + 1;
              tsPairs2.Delete(j);
              Break;
           end;
        end;
     end;
     Result := 2.0*iIntersection/iUnion;
  finally
     // tidy up
     freeandnil(tsPairs1);
     freeandnil(tsPairs2);
  end;
end;